BSc Thesis: Calculating Mutual Information in Metric Spaces

Old Laurels

My final-year individual project at Bristol with Dr. Conor Houghton is my highest academic achievement so far. Through it, I learned how to conduct scientific research and computational experiments. Further, I gained the invaluable experience of being occupied with a very narrow and specialized domain of knowledge at the frontier of science.

The purely mathematical simplicity (and fundamental ingenuity) of Conor's formula made it possible for me to tackle the problem. Its application to our understanding of how the brain works (which is still very limited) motivated me to succeed. It also qualified as contribution to science by the university's assessment citeria - it was graded above 80% (85%) - and this was utterly satisfying!

Abstract

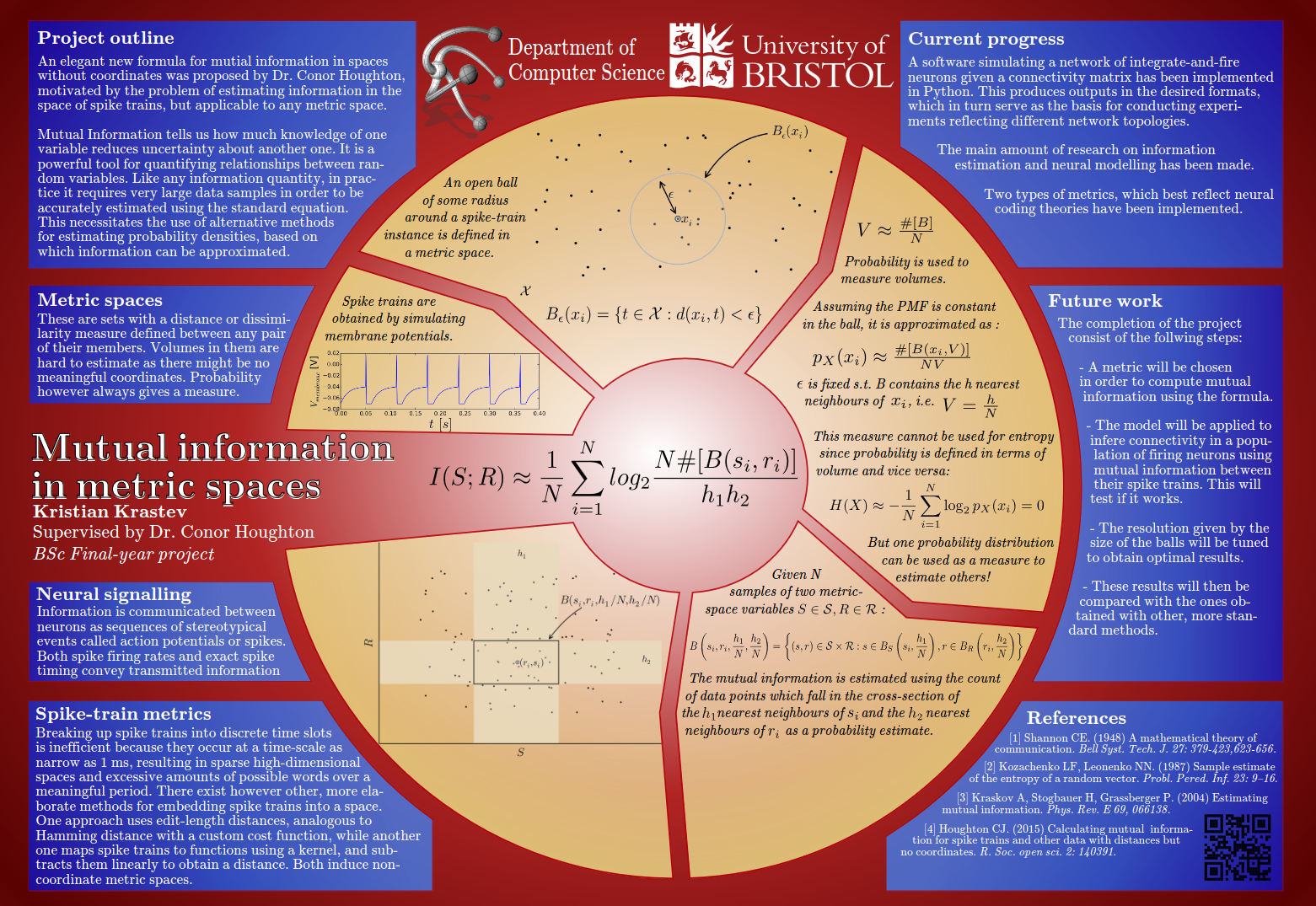
Mutual information tells us how much the uncertainty associated with one variable is reduced by the knowledge of another one [18, 2]. It is a useful tool for quantifying relationships and has many applications to statistical modelling - for example in various types of clustering where one aims to maximise the dependencies within a partition. Typically, like most information-theoretic quantities, mutual information is estimated for variables that are either discrete or take values in a coordinate space. However, many important data types have distance metrics or measures of similarity, but no coordinates on them. The spaces induced by these metrics are not manifolds and their integration measure is not so obvious. Datasets of this type are collected from electrophysiological experiments in neuroscience and gene expression data in genetics and biochemistry, but also in other fields like image analysis and data retrieval.

The purpose of this project was to implement and test an estimator for calculating mutual information between data, where one or both variables come from a metric space without coordinates. The model estimator itself was been described in [27], but had not been implemented and tested until now. It aims to provide a simple approach to the Kozachenko-Leonenko estimator for mutual information [5], that extends it in order to apply to the broader class of metric-space data.

The model is particularly relevant to neuroscience because it addresses the problem of calculating information theory quantities from the similarity measures on the space of spike trains. This is the application that motivates it and serves as the main framework for producing the data, used to test and adjust it.

Application software was developed in Python2. It was the preferred choice over MATLAB for example, because it is a modern high-level language with nice syntax and structure that supports various coding styles. It also has libraries and packages which are analogous to the MATLAB functionality relevant to the task: NumPy, SciPy, PyLab, matplotlib etc. In addition to this, it offers interfaces to other tools for computational neuroscience and mathematics, which could be useful for the future development of the project. The implementation applies the suggested model to fictive spike-train data generated using a stochastic model and data related to it that is produced by a deterministic neural simulation. The proposed thesis aims to investigate the model's correctness and evaluate its performance on various tasks. The analysed results paved the way to its future application to real experimental neuroscientific data.

Context

Undertaking the problem involved multiple levels of mathematical abstraction and modelling at the intersection of Computer Science, Mathematics and Computational Neuroscience. Its objective was to demonstrate empirically that the estimator works by simulating a simplified model of biological neurons' spiking behaviour, upon input signal reception from artificially generated stimulus data.

Unsurprisingly, the biggest challenge was convincing the examiners that the experimental result led to valid conclusions without being compared to a ground truth or the go-to estimtion method (due to its computational cost and the time limitations for my thesis).

In 2015 I switched to a 3-year BSc from a 4-year MEng course after retaking the DSA module between 2^nd and 3^rd years at UNI. I wanted to graduate together with my peers and to do a scientific thesis instead of taking part in a 3^rd-year game-dev group project.

Apart from studying algorithms, during my gap year I split my time between visiting my friends' 3^rd-year and masters' classes, working as part of Bristol Sicence Museum's catering staff, and engaging in long discussions on math topics with my friend Dr. Delyan Savchev who was doing a PhD in Probability & Statistics at the time. Thanks to his guidance I was able to persuade Conor, who was my personal tutor to direct me towards a hard problem within his research domain and supervise my final-year project.

Conclusion

The aim of this project was to implement and test a model for estimating mutual information in metric spaces without coordinates in the context of computational neuroscience. The process of achieving this involved extensive research on the mathematical and information-theoretic grounds for its emergence, the metric-space framework for computing spike-train distances it relies on, and the computational methods for simulating neural signalling behaviour.

A neural simulation environment was developed in software to serve as the basis for constructing experiments designed to test the estimator. Two types of cutting-edge spike-train metrics have been implemented. It was demonstrated that probability densities can be successfully estimated using nearest-neighbour statistics in the metric spaces induced by these similarity measures. The implemented information estimator is simple and elegant and provides a novel direct way of estimating information-theoretic quantities depending on the probability distributions of more than one variables taking values in metric spaces.

The neuroscientific problem of calculating mutual information has no analytical solution to test the estimates against. The alternative estimation technique is effectively cumbersome and operates on a different principle risking to fit the space of spike-trains into the Procrustean bed of direct time discretisation. Therefore a strategy was devised for the verification of mutual information estimates based on criteria reflecting their implicit relationship to simulation parameters. Additionally, the nearest-neighbour resolution was investigated and the convergence of the estimates was tested on increasing amounts of input data under constant experimental conditions. Traditional correlation analysis has been used to quantify linear relationships along with the least-squares linear regression model. Both the Pearson correlation coefficient and the mutual information estimates were demonstrated to exhibit convergence behaviour.

The implications of the presented results to information-theoretic analysis in spaces with non-manifold geometry are yet to unfold. Here they served as a practical proof for the concept of using the marginal probability distribution of one variable as an integration measure in the metric space of another one to some approximation. We have seen this idea develop progressively through the work of Kozachenko and Leonenko [5], Kraskov, Stoegbauer and Grassberger [17], and Houghton and Tobin [27, 23].

The software and results produced during this year-long project will be used for its further development during the summer period. A version of the estimator for the case when one of the variables is coming from a discrete corpus has already been implemented and applied to real experimental data recording neural signals of a laboratory mouse running in a maze. Other, initially intended extensions have not been developed entirely to this point and are yet to be completed. The problem and its solution open up an array of possibilities for research and applications. And while this concludes the current work it will be interesting to continue exploring the topic.

Aftermath

I did not progress substantially with subsequent research during the follow-up summer internship at the computational neuroscience research lab. The goal was to benchmark the new formula together with the traditional method by Bialek [11]. The main stopper was my lack of experience in HPC, coupled with the time-scarcity to gain thereof. I did however manage to imporve the code and convergence analysis a bit.

Although I haven't contributed any scientific work ever since, this thesis taught me a lot of mathematics but, most importantly, how to read papers and do research on my own which was truly useful later on in my work as ML/AI engineer and data scientist.

References